
Project ANR JCJC HASCON (2019 -
2023)
Harmonic Analysis for Semigroups on Commutative
and Non-commutative Lp spaces
Version française
Contact : 
Contents
1 Members
- Cédric Arhancet
- Luc Deleaval
- Adrián González-Pérez (postdoctorant year 2019-2020)
- Christoph Kriegler (project coordinator)
2 Key words of research
- Harmonic Analysis
- Semigroups of operators
- Non-commutative geometry
- Functional calculus
- Maximal operators
- Non-commutative Lp spaces
- Operator spaces
- Riesz transforms
- Singular integrals
- Geometry of Banach spaces
- Fourier multipliers on groups and Schur multipliers
- R-boundedness
3 Presentation of the project
Since the fundamental works of Stein and Cowling, the spectral theory for
semigroups has become a wide mathematical field and a lot of mathematicians work
in that field today. Much progress has been achieved over the last four decades, many
beautiful connections have been proven to be fruitful in solving problems
inside and outside harmonic analysis. The aim of our project HASCON is
to answer the following questions, which arise in the context of spectral
theory, functional calculus, harmonic analysis or abstract partial differential
equations:
- Under which circumstances (e.g. which underlying classical or
non-commutative Lp or Banach space) does the generator of a semigroup
admit an H∞ or Hormander(-Mihlin) functional calculus? This is a
property well-known to be of great importance in theoretical aspects and
for many applications. The answer depends on the underlying space X,
which can consist of functions over some measure space Ω (often Lp(Ω)),
or also be a non-commutative Lp space, i.e. a space of (un)bounded
operators affiliated with a von Neumann algebra. Hereby, geometrical
properties of the Banach space X usually play an important rôle, and
we give a particular emphasis to Bochner spaces X = Lp(Ω,Y ). Then
the property of Y being a UMD space becomes important, and also
its Rademacher-type and -cotype as well as related notions such as
p-convexity and q-concavity if Y is moreover a lattice. Our motivation for
Bochner spaces comes from their importance in applications to abstract
Cauchy problems, where Y takes over the rôle of a spatial variable,
whereas the time variable is the parameter t of the semigroup Tt; for
square function estimates, where Y = ℓ2 (then the interesting functional
calculus question involves a sequence of spectral multipliers (fk)k); and
lastly for descriptions of abstract function spaces associated with the
generator, such as Sobolev and Triebel-Lizorkin spaces, where Y = ℓq.
- For which cases is an evolution maximal operator, in the most classical
form MTf = supt>0|Ttf| or spatial maximal operator MHLf =
supr>0
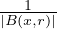 ∫
B(x,r)|f(y)|dy bounded? This and the above functional
calculus question are closely linked and reinforce each other. Namely,
on the one hand, an H∞ calculus with a good angle allows to extend
the boundedness of the evolution maximal operator on Lp(Ω) above
to a sectorial maximal operator. Then under the presence of integral
kernel estimates of Tt, evolution and spatial maximal operators are
simultaneously bounded. On the other hand, boundedness of a maximal
operator plays sometimes a crucial tool in establishing H∞ calculus
and Hormander-Mihlin calculus. Again we pay a particular attention to
Bochner-space valued boundedness of MHL,MT. From a general point
of view, standard maximal operators are important in several branches
of harmonic and real analysis (e.g. singular integrals, multipliers,
Littlewood-Paley theory).
∫
B(x,r)|f(y)|dy bounded? This and the above functional
calculus question are closely linked and reinforce each other. Namely,
on the one hand, an H∞ calculus with a good angle allows to extend
the boundedness of the evolution maximal operator on Lp(Ω) above
to a sectorial maximal operator. Then under the presence of integral
kernel estimates of Tt, evolution and spatial maximal operators are
simultaneously bounded. On the other hand, boundedness of a maximal
operator plays sometimes a crucial tool in establishing H∞ calculus
and Hormander-Mihlin calculus. Again we pay a particular attention to
Bochner-space valued boundedness of MHL,MT. From a general point
of view, standard maximal operators are important in several branches
of harmonic and real analysis (e.g. singular integrals, multipliers,
Littlewood-Paley theory).
- What kind of operations on non-commutative Lp spaces yield bounded
and completely bounded maps? The most prominent examples of
such mappings important in harmonic analysis are Schur multipliers,
non-commutative Fourier multipliers or operations stemming from
second quantization, such as q-Ornstein-Uhlenbeck semigroups. Schur
multipliers provide a surprisingly rich class of mappings and they have
a longstanding usage in various fields of analysis such as complex
function theory, Banach spaces, operator theory, multivariate analysis,
theory of absolutely summing operators and functional calculus. Fourier
multipliers on non-commutative groups and second quantizations are
a rather new field in harmonic analysis. Non-commutative harmonic
analysis involves more algebraic and also combinatoric structure.
4 Events
There has been a two days meeting of the ANR project Thursday 20 October -
Friday 21 October 2022 entitled
Harmonic Analysis of semigroups on commutative and non-commutative Lp
spaces.
It took place at Université Gustave Eiffel, Marne-la-Vallée, France. The aim of the
conference was to bring together mathematicians working on harmonic analysis
techniques which have been proven fruitful in the Lp-theory of operators (functional
calculus, operator semigroups, maximal operators, square functions) – and in recent
times could be successfully adapted to non-commutative counterparts such as Fourier
multipliers on l.c. groups and Schur multipliers. There were four presentations of 60
min and seven of 30 min, and as usual also time for discussions was left. The schedule
was the following.
| | Thursday 20 October 2022 |
| 9h00 – 9h30 | Reception of the participants at LAMA = coffee break 1 |
| 9h30 –10h30 | Wolfgang Arendt |
| 10h45 – 11h45 | Mariusz Mirek |
| 12h00 – 14h00 | Lunch |
| 14h00 –14h30 | Blazej Wróbel |
| 14h30 – 15h00 | Oliver Dragičević |
| 15h00 – 15h30 | Coffee break 2 |
| 15h30 – 16h00 | Emiel Lorist |
| 16h00 – 16h30 | Nick Lindemulder |
| 16h30 – 17h00 | Tomasz Szarek |
| 20h00 | Conference dinner |
| | Thursday 21 October 2022 |
| 09h30 – 10h30 | El Maati Ouhabaz |
| 10h30 – 11h00 | Coffee break 3 |
| 11h00 – 11h30 | Cédric Arhancet |
| 11h30 – 12h00 | Léonard Cadilhac |
| 12h00 – 14h00 | Lunch |
| 14h00 – 15h00 | Mark Veraar |
The following is the list of participants as of 28/09/2022.
- Benjamin Arras
- Sebastian Bechtel
- Clément Coine
- Lukas Hagedorn
- Kamal Khalil
- Fatima Zahra Lahbriri
- Christian Le Merdy
- Éric Ricard
- Silvia Romanelli
- Elizabeth Strouse
- Alexandre Thorel
- Safoura Zadeh
5 Publications and Preprints
- L. Deléaval and C. Kriegler: Dunkl spectral multipliers with values in
UMD lattices, Journal of Functional Analysis, 272(5):2132–2175, 2017.
Preprint here and on HAL.
- L. Deléaval and C. Kriegler: Dimension free bounds for the vector-valued
Hardy-Littlewood maximal operator, Rev. Mat. Iberoam., 35(1):101–123,
2019. Preprint on HAL, arxiv.org.
- L. Deléaval, M. Kemppainen and C. Kriegler: Hörmander functional
calculus on UMD lattice valued Lp spaces under generalised Gaussian
estimates, Journal d’Analyse Mathématique, 145(1), 177–234, 2021.
Preprint here, on HAL and on arXiv.org.
- C. Arhancet and C. Kriegler: Complementation of the subspace of
radial multipliers in the space of Fourier multipliers on ℝn, Archiv der
Mathematik, 112(1), 93–100, 2019. Preprint on HAL, arXiv.org.
- C. Arhancet and C. Kriegler: Projections, multipliers and decomposable
maps on noncommutative Lp-spaces, Mémoires de la Société
Mathématique de France, 177 (new series). Preprint on HAL and on
arXiv.org.
- C. Arhancet and C. Kriegler: Riesz transforms, Hodge-Dirac operators
and functional calculus for multipliers, Springer Lecture Notes in
Mathematics, 2304. Springer, 2022, Cham, xii+278 pp. Preprint on HAL
and on arXiv.org.
- C. Arhancet: Dilations of markovian semigroups of Fourier multipliers on
locally compact groups, Preprint on arXiv.org.
- K. Domelevo, C. Kriegler and S. Petermichl: H∞ calculus for
submarkovian semigroups on weighted L2 spaces Mathematische
Annalen, 381(3-4), 1137–1195, 2021. Preprint on HAL and arXiv.org.
- C. Arhancet: Positive contractive projections on noncommutative
Lp-spaces and nonassociative Lp-spaces, Preprint on arXiv.org.
- C. Arhancet: Contractively decomposable projections on
noncommutative Lp-spaces, Preprint on arXiv.org.
- C. Arhancet: Dilations of markovian semigroups of measurable Schur
multipliers, Preprint on arXiv.org.
- J. Conde-Alonso, A. González-Pérez and J. Parcet: Noncommutative
strong maximals and almost uniform convergence in several directions,
Forum Math. Sigma 8, Paper No. e57, 39 p. (2020). Preprint on arXiv.org.
- L. Deléaval, N. Demni: Generalized Bessel functions of dihedral-type:
expression as a series of confluent Horn functions and Laplace-type
integral representation, Ramanujan J. 54, No. 1, 197-217 (2021).
- S. Ben Saïd. and L. Deléaval: Translation operator and maximal function
for the (k,1)-generalized Fourier transform, J. Funct. Anal. 279, No. 8,
Article ID 108706, 31 p. (2020).
- C. Arhancet: Contractively decomposable projections on
noncommutative Lp-spaces, Preprint on arXiv.org, submitted.
- C. Arhancet and Yves Raynaud: 2-positive contractive projections on
noncommutative Lp-spaces, submitted.
- C. Arhancet: A characterization of completely bounded normal Jordan
*-homomorphisms on von Neumann algebras, submitted.
- C. Arhancet: Quantum information theory and Fourier multipliers on
quantum groups, submitted, Preprint on arxiv.org.
- L. Deléaval and C. Kriegler: Maximal Hörmander Functional Calculus
on Lp spaces and UMD lattices, International Mathematical Research
Notices, Preprint on HAL, on arXiv.org and here.
- C. Arhancet: Dilations of semigroups on von Neumann algebras and
noncommutative Lp-spaces, J. Funct. Anal., 276, No. 7, 2279-2314
(2019).
- L. Deléaval and C. Kriegler: q-variational Hörmander functional calculus
and Schrödinger and wave maximal estimates, Preprint here.
- C. Arhancet, C. Kriegler, C. Le Merdy and S. Zadeh: Separating Fourier
and Schur multipliers. Accepted for publication in Journal of Fourier
Analysis and Applications. Preprint on HAL and on arXiv.org.
- C. Arhancet and C. Kriegler: Fourier-Stieltjes algebras, decomposable
Fourier multipliers and amenability. Preprint on arXiv.org.
- A. González-Pérez: Lower bounds in Lp-transference for crossed
products. Preprint on arXiv.org.
- A. González-Pérez, J. Parcet and R. Xia: Noncommutative Cotlar
identities for groups acting on tree-like structures. Preprint on arXiv.org.
- S. Ben Saïd and L. Deléaval: A Hardy-Littlewood maximal operator
for the generalized Fourier transform on ℝ. J. Geom. Anal. 30, No. 2,
2273-2289 (2020).
- C. Arhancet: Spectral triples, Coulhon-Varopoulos dimension and heat
kernel estimates. Submitted. Preprint on arXiv.org.
- C. Arhancet: Sobolev algebras on Lie groups and noncommutative
geometry. Submitted. Preprint on arXiv.org.
Website updated on 01/02/2024.



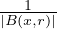 ∫
B(x,r)|f(y)|dy bounded? This and the above functional
calculus question are closely linked and reinforce each other. Namely,
on the one hand, an H∞ calculus with a good angle allows to extend
the boundedness of the evolution maximal operator on Lp(Ω) above
to a sectorial maximal operator. Then under the presence of integral
kernel estimates of Tt, evolution and spatial maximal operators are
simultaneously bounded. On the other hand, boundedness of a maximal
operator plays sometimes a crucial tool in establishing H∞ calculus
and Hormander-Mihlin calculus. Again we pay a particular attention to
Bochner-space valued boundedness of MHL,MT. From a general point
of view, standard maximal operators are important in several branches
of harmonic and real analysis (e.g. singular integrals, multipliers,
Littlewood-Paley theory).
∫
B(x,r)|f(y)|dy bounded? This and the above functional
calculus question are closely linked and reinforce each other. Namely,
on the one hand, an H∞ calculus with a good angle allows to extend
the boundedness of the evolution maximal operator on Lp(Ω) above
to a sectorial maximal operator. Then under the presence of integral
kernel estimates of Tt, evolution and spatial maximal operators are
simultaneously bounded. On the other hand, boundedness of a maximal
operator plays sometimes a crucial tool in establishing H∞ calculus
and Hormander-Mihlin calculus. Again we pay a particular attention to
Bochner-space valued boundedness of MHL,MT. From a general point
of view, standard maximal operators are important in several branches
of harmonic and real analysis (e.g. singular integrals, multipliers,
Littlewood-Paley theory).