
| ACCUEIL |
C.V. |
RECHERCHE |
PUBLICATIONS |
SIMULATIONS |
ENSEIGNEMENTS |
LOISIRS |
 POLE DE MATHÉMATIQUES |
Quelques animations...
Laurent Chupin Enseignant-chercheur --- Mathématiques |
 INSTITUT CAMILLE JORDAN |
MÉLANGE DE FLUIDES VISCO-ÉLASTIQUES • • • Une référence pour en savoir plus : [ref]
Les fluides dont la contrainte
est déterminée par la pression seule sont appelés
des fluides
parfaits. Le modèle sous-jacent est décrit par
l'équation d'Euler,
déterminée au cours du XVIII-ème
siècle. Au milieu du XIX-ème siècle, Stokes et
Navier propose de prendre en compte des effets visqueux qu'ils
quantifient par l'expérience. Bien que de nombreux fluides
peuvent effectivement être considérés comme
visqueux (on les appelle des fluides newtoniens), certains fluides ne
suivent pas ces lois "linéaires". De nombreux
modèles plus ou moins complexes ont alors vu le jour...
Un fluide visco-élastique est un de ces fluides. Pour ces
modèles, on considère non seulement que le fluide est
visqueux mais aussi qu'il est élastique, autrement dit qu'il
possède une mémoire.
Et voici ce qu'on peut simuler en mélangeant deux fluides
visco-élastiques :|
Fluide newtonien |
Un peu visco-élastique |
Très élastique |
Les
simulations ci-dessous mettent en lumière le
phénomène de décomposition spinodale :
si la température passe sous une valeur critique, deux fluides
bien
mélangés se séparent. Si on leur impose en plus un
cisaillement, ils s'alignent en formant des bandes. Cette
théorie est validée ici pour des fluides newtoniens mais
pas pour des fluides visco-élastiques.
Mélange newtonien - Mélange visco-élastique |
PRESSION DE FLUIDE DANS DES MÉCANISMES LUBRIFIÉS • • • Une référence pour en savoir plus : [ref]
La description du
logiciel développé puis utilisé pour obtenir ces
simulations est dispo-
-nible ici ou sur le site du projet PLUME http://www.projet-plume.org/fr/relier/elvis
Dans des mécanismes de
lubrification (comme par exemple dans des
roulements à billes), les fluides sont soumis à de fortes
contraintes liées à la pression interne aux fluides. Il
est
important de pouvoir calculer ces pressions efficacement :
c'est-à-dire rapidement et précisement. Un des
systèmes de base pour modéliser ce type
d'écoulement correspond aux équations de Reynolds. Ces
équations ne sont rien d'autre que les équations de
Navier-Stokes dans lesquelles on a conservé uniquement les
premiers termes d'un développement
limité en fonction du rapport hauteur du domaine/longueur du
domaine (en effet, dans les études de lubrification ce rapport
est souvent très petit, de l'ordre de 0.001).-nible ici ou sur le site du projet PLUME http://www.projet-plume.org/fr/relier/elvis
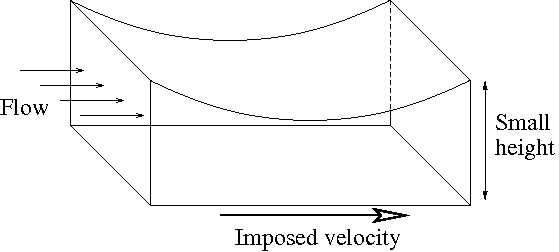 Le domaine dans lequel
s'écoule le fluide est schématisé par la figure
ci-dessus. L'écoulement est confiné entre deux plaques :
celle du haut
au repos qui contient toute la géométrie du domaine,
et celle du
bas plane mais qui est animée d'une vitesse imposée.
|
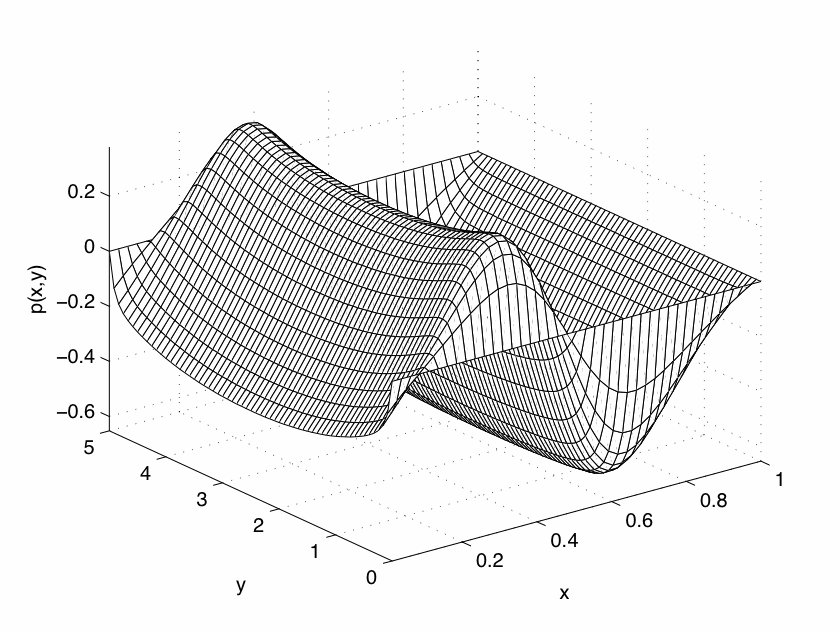 Fig 1 : Cas newtonien (0% d'élasticité) |
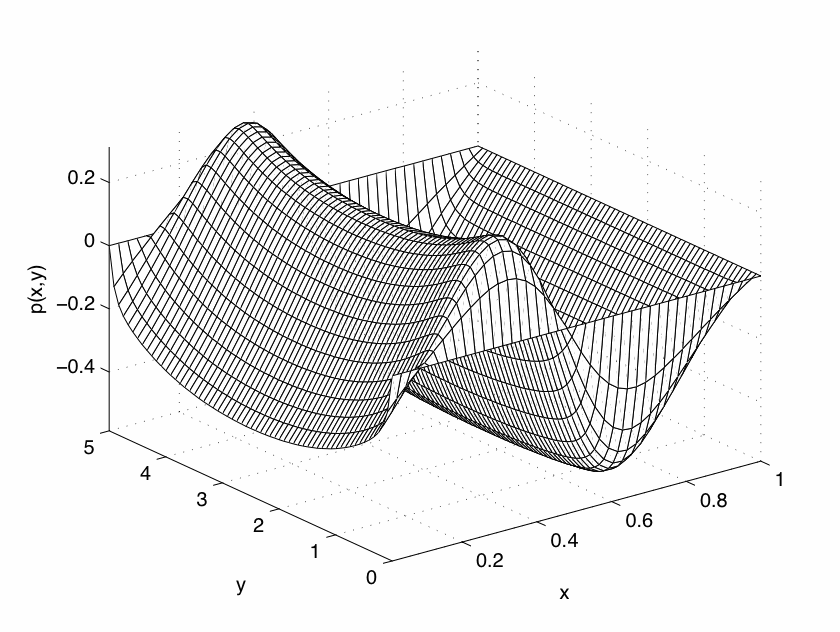 Fig 2 : Cas peu élastique (20%) |
|
Dans les simulations
suivantes, on impose un débit
de vitesse en amont puis on observe les pressions obtenues. La
géométrie est fixée et nous avons fait varier
uniquement les propriétés d'élasticité du
fluide.
• La figure 1 correspond
aux cas d'un fluide newtonien
(c'est-à-dire purement visqueux, sans aucune
propriété d'élasticité). Elle
représente les valeurs de la pression dans le domaine.
• Dans les trois autres figures, nous avons simplement introduit de plus en plus délasticité dans le modèle. |
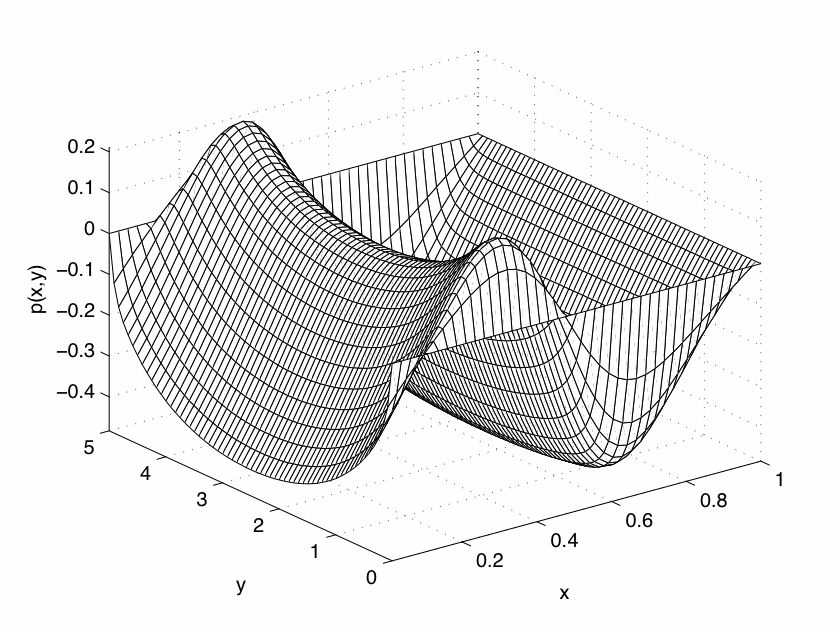 Fig 3 : Cas visco-élastique (50%) |
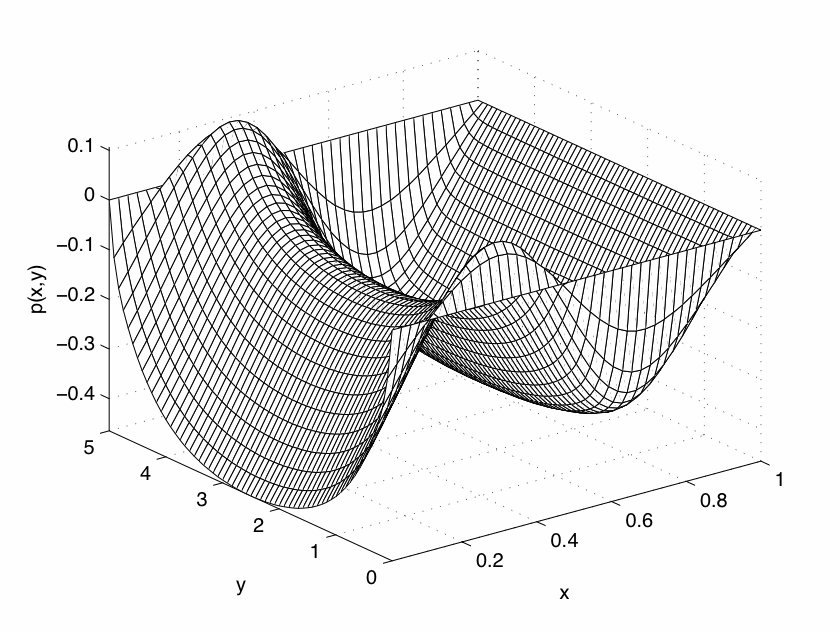 Fig 4 : Cas très élastique (80%) |
DISTRIBUTION DE RESSORTS DANS UN ÉCOULEMENT DE POLYMÈRES • • • Une référence pour en savoir plus : [ref]
Le modèle FENE (finite
extensibility non linear elasticity) est
utilisé pour modéliser le comportement du tenseur des
contraintes dans certains type de fluides visco-élastiques
(essentiellement les solutions de polymères diluées).
Comme son nom l'indique, le modèle schématise les
chaînes de polymères par des ressorts qui ont une longueur
maximale. Initialement, le modèle est plutôt vu comme un
modèle probabiliste (formé d'équations
différentielles stochastiques) et prend en compte des impacts
stochastiques de nature brownienne sur les chaînes de
polymères. C'est la version "équation aux
dérivées partielles" équivalente que j'ai un peu
étudié.
 |
 |
 |
|
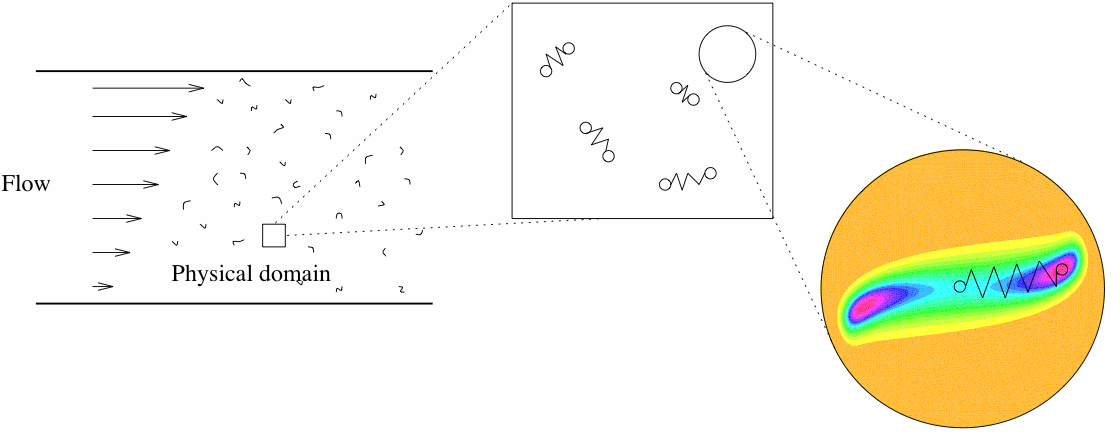
| A
gauche, le domaine
physique d'un écoulement réel : le champ de vitesse est
donné (on suppose par exemple que le champ de vitesse est un
champ de cisaillement comme représenté sur la figure). Au point de vue microscopique, on identifie les chaînes de polymères à des systèmes masses-ressorts. L'orientation et la longueur de chaque ressort est une quantité distribuée dans une boule dont le rayon correspond à l'extension maximale du ressort. A droite, les couleurs correspondent aux différentes probabilités qu'un ressort soit dans la position donnée. Pour le dessin donné ici, le ressort dessiné est celui qui à le plus de chance d'être présent. |
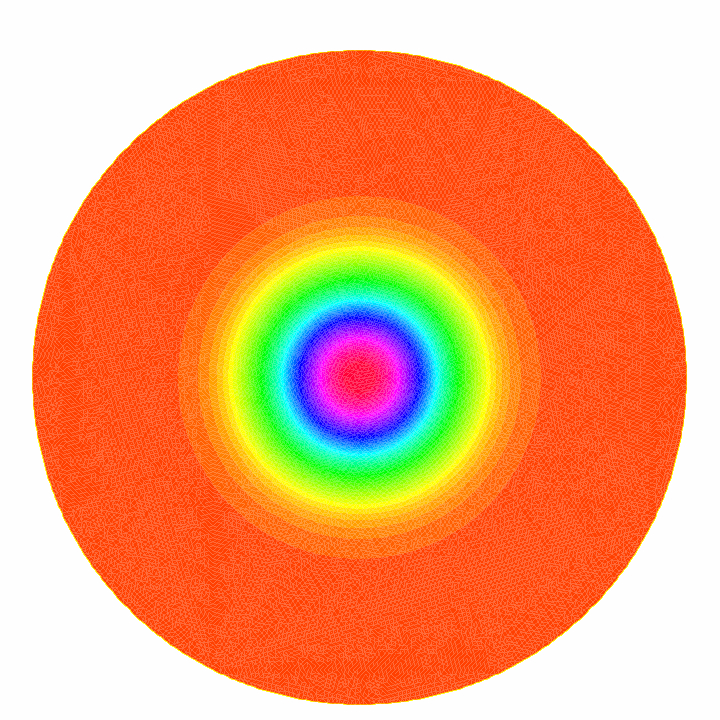
Fig 1
Le fluide est au
repos (sans cisaillement), les ressorts sont distribués
"régulièrement". |
Fig 2 Film de l'évolution de la distribution des ressorts lorsque la vitesse de cisaillement varie. |
Fig 3 Lorsque la vitesse de cisaillement est très grande, les ressorts ont tendance à s'étirer et à s'aligner tous dans la direction principale de l'écoulement. |
EFFETS DES RUGOSITÉS DANS DES ÉCOULEMENTS MINCES • • • Une référence pour en savoir plus : [ref]
Le contexte physique
étudié ici est similaire à
celui présenté plus haut (au sujet de la pression dans
des mécanismes lubrifiés). Nous avons proposé un
modèle très simple à résoudre
numériquement et permettant de prendre en compte des
rugosités dans des écoulements minces et
cisaillés. Ce modèle correspond à l'approximation
au premier ordre des équations de Navier-Stokes
tridimensionnelles lorsque le domaine où s'écoule le
fluide est infiniment mince (d'ordre µ<<1), et comporte des
zones
"rugueuses". Les rugosités sont schématisées par
le bord du domaine décrit par des fonctions oscillantes (de
fréquence et d'amplitude très petites µ²).
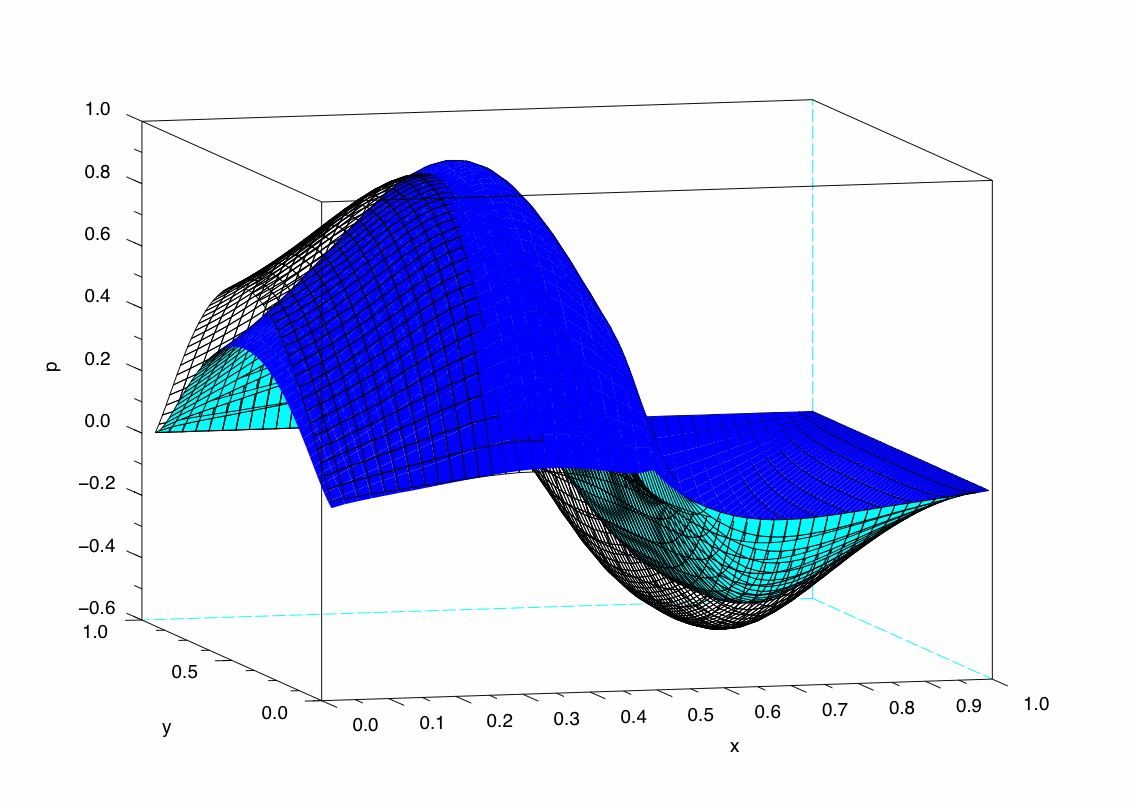 Fig 1 : Effet des rugosités à gauche 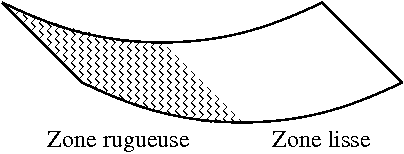 |
Dans les deux exemples
présentés ici (à gauche et à droite), j'ai
tracé en quadrillage la solution sans aucune rugosité. En
bleu correspondent les solutions avec des rugosités sur une
partie du haut du domaine.
 |
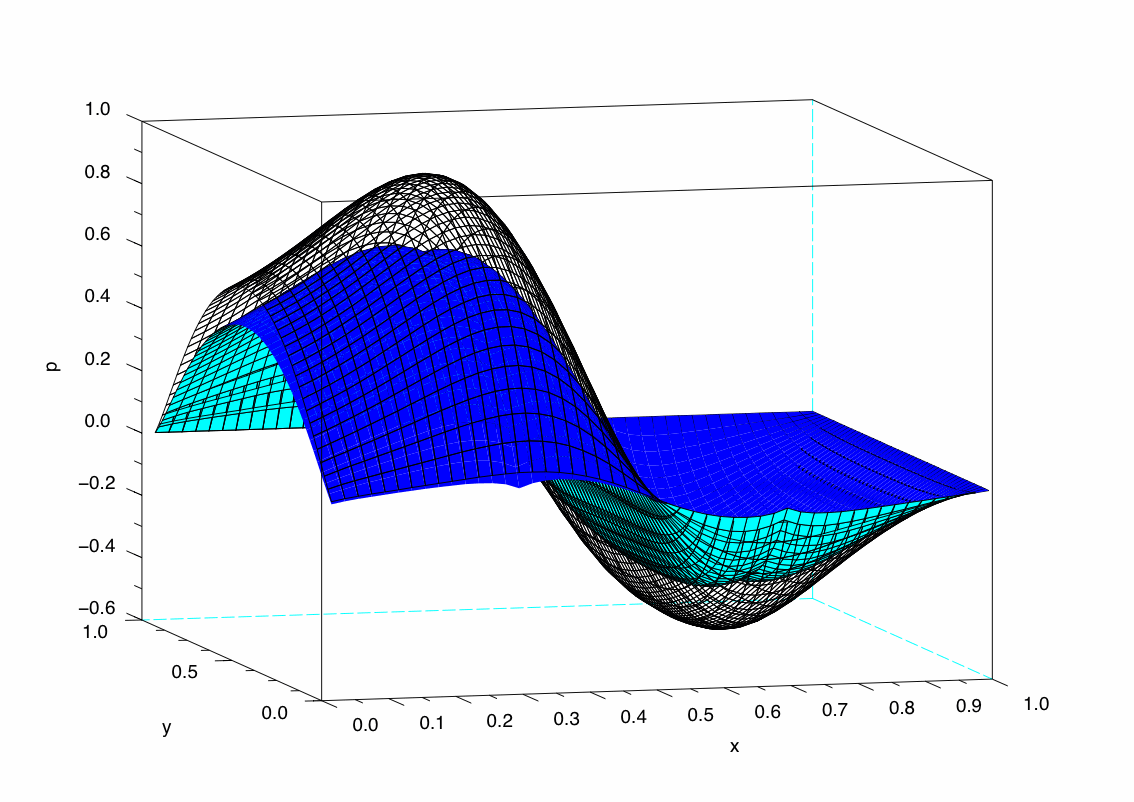 Fig 2 : Effet des rugosités au milieu 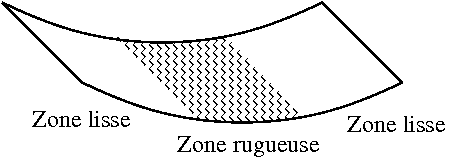 |
| © Laurent Chupin - Institut Camille Jordan - Pôle de Mathématiques |