Is sometimes useful to have a regular function close to the characteristic function of an interval.
More precisely, we want a \(C^\infty\) function \(\chi_{a, b, \delta} : \mathbb{R} \to \mathbb{R}\) verifying:
- \(\text{supp}(\chi_{a, b, \delta}) = (a, b)\)
- \(\chi_{a, b, \delta}(x) = 1\) for every \(x \in [a+\delta, b - \delta]\).
An example of such a function is the following one:
\begin{equation*} \chi_{a,b, \delta}(x) = \left\{ \begin{array}{ll} 0 &\qquad \text{if } x \notin (a, b) \\ 1 &\qquad \text{if } x \in [a + \delta, b-\delta] \\ \frac{1}{2} + \frac{1}{2}\tanh\left(\tan\left(-\frac{\pi}{2} + \frac{x - a}{\delta}\pi\right)\right) & \qquad \text{if } x \in (a, a+\delta) \\ \frac{1}{2} + \frac{1}{2} \tanh\left(\tan\left(\frac{\pi}{2} - \frac{x - b + \delta}{\delta}\pi\right)\right) & \qquad \text{if } x \in (b-\delta, b) \end{array} \right. \end{equation*}
Bellow is a python implementation of this function
import numpy as np
def cutoff(x, a, b, d):
y = 1.0 * (x >= a + d) * (x <= b - d)
i = np.argwhere((x > a) * (x < a + d))
y[i] = y[i] + 0.5 + 0.5*np.tanh(np.tan(-np.pi/2 + (x[i] - a)/d*np.pi))
i = np.argwhere((x > b-d)*(x < b))
y[i] = y[i] + 0.5 + 0.5*np.tanh(np.tan(np.pi/2 - (x[i] - b + d)/d*np.pi))
return y
and its graphic representation for \(a = 0.2\), \(b = 0.8\) and \(\delta = 0.2\).
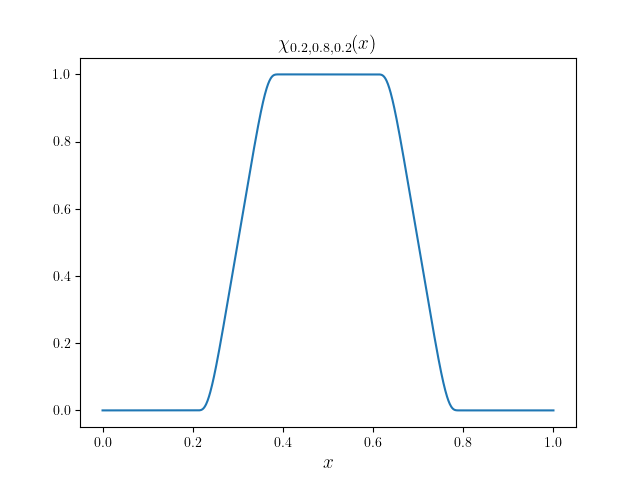
Figure 1: Graphic representation of \(\chi_{0.2, 0.8, 0.2}\)